Introduction
Maths is a fundamental part of Data Science: calculus, statistics, probability theory and other mathematical topics are used in the approaches we apply at work daily. Even though all the mathematical equations are usually implemented under the hood of the libraries we use, it’s important to understand the basics to be able to solve problems that are a bit more complex than just applying some predefined function. That’s why maths questions are often asked in Data Science interviews.
In the article below, you will find four maths problems that I was asked in real interviews for Data Science jobs. Try to solve them before you read the solutions! 😉
Problems
Pedestrians and a Dog
Problem Statement
A and B are two points located 3 km apart. Two pedestrians start walking towards each other from points A and B at a speed of 5 km/h. At the same time, a dog starts running from point A at a speed of 10 km/h. When the dog reaches one of the pedestrians, it immediately turns around and runs toward the other pedestrian. This continues until all three of them meet.
What is the distance covered by the dog before they meet?
Problem Solution
It sounds like a classic school problem dealing with speed and distance. Although it’s a bit tricky because the dog changes direction and it’s quite hard to calculate the distance before each turn to sum them up.
Let’s start with the basics: we need to find the Distance, what is the formula for it?
$$Distance=Speed*Time$$
We know the Speed from the problem statement. Can we find out the Time?
The Time of the dog running is the time it takes for all three to meet. If the pedestrians are walking at a speed of 5 km/h and the distance between them is 3 km, they will meet in 3 / (5 + 5) = 0.3 hours.
It looks like we have all the pieces we need for the Distance formula:
$$Distance=Speed * Time = 10 * 0.3=3 km$$
A Defective Coin
Problem Statement
There are 100 coins in a bag, one of which is defective (heads on both sides). A coin is drawn at random, and tossed twice, both times coming up heads.
What is the probability that the coin is defective?
Problem Solution
This is a classic conditional probability problem. In this case, we need to use Bayes' theorem:
$$P(A|B) = \frac{P(B|A) * P(A)} {P(B)}$$
In our case, events A and B are as follows:
A: The coin is defective;
B: The coin came up heads after both tosses.
Let’s rewrite the formula, replacing the event names with Def for Defective and 2H for two heads:
$$P(Def|2H)=\frac{P(2H|Def) * P(Def)}{P(2H)}$$
Let’s then calculate each probability separately:
P(2H|Def) is the probability of seeing two heads when the coin is defective, which is always true: P(2H|Def) = 1;
P(Def) is the probability that the coin is defective, which is P(Def) = 1 / 100;
P(2H) is the probability of seeing two heads after two tosses:
We should consider two separate cases here:
The coin is defective: in this case, P(2H|Def) = 1 as discussed above and the probability of drawing the defective coin from the bag is P(Def) = 1 / 100;
The coin is not defective (normal): in this case, P(2H|Norm) = (1 / 2) * (1 / 2) = 1 / 4 and the probability of drawing a normal coin from the bag is P(Norm) = 99 / 100;
Now we can calculate P(2H):
$$\begin{aligned} P(2H) &= P(Def) * P(2H|Def) + P(Norm) * P(2H|Norm) = \\ &=\frac{1}{100} * 1 + \frac{99}{100} * \frac{1}{4} = \frac{103}{400} \end{aligned}$$
It looks like we have all the ingredients for our initial formula:
$$P(Def|2H)=\frac{P(2H|Def) * P(Def)}{P(2H)}=\frac{1*\frac{1}{100}}{\frac{103}{400}}\approx0.0388$$
Quadratic Equation
Problem Statement
Consider the quadratic equation x^2 + bx + c = 0, where b and c are uniformly distributed in the range [0, 1].
What fraction of the values of b and c gives a solvable equation?
Problem Solution
A quadratic equation has a solution if its discriminant is not negative. Let’s write down the discriminant:
$$D = b^2-4ac$$
where a is the coefficient of x^2, which in our case is equal to 1.
Now let's do some transformations:
$$D ≥ 0 \Leftrightarrow b^2 - 4c ≥ 0 \Leftrightarrow c ≤ \frac{b^2}{4}$$
And plot the function:
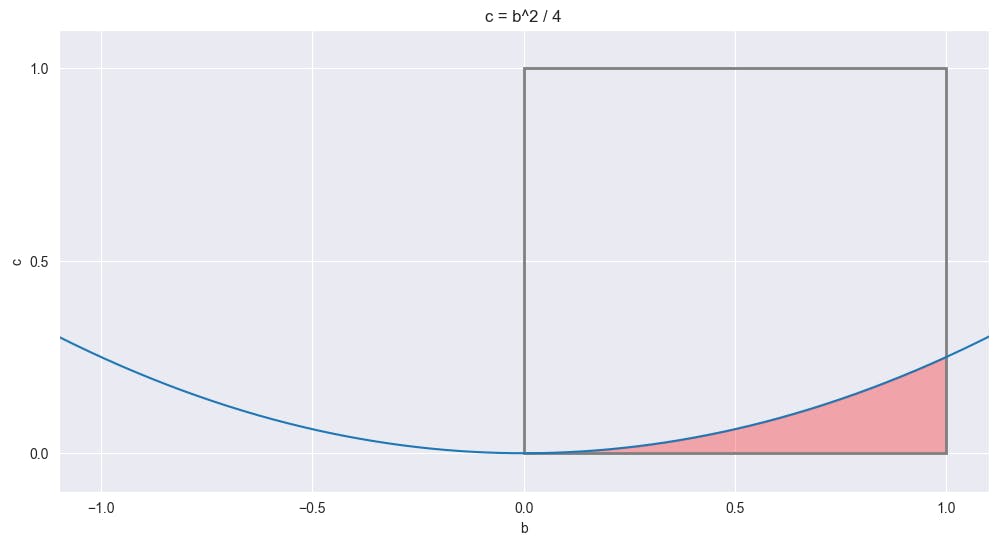
b and c are defined in the range between 0 and 1 (grey square). As explained above, we are interested in the values where c ≤ b^2 / 4 - that’s the red area on the plot.
To find the red area, we need to calculate the following integral:
$$\int_{0}^{1}\frac{b^2}{4}db=\frac{b^3}{12}\Big|_0^1=\frac{1}{12}\approx0.083$$
In answer to the initial question, 8.3% of the b and c values give us a solvable equation.
Expected value of a Minimum of Two Random Variables
Problem Statement
A and B are independent and identically distributed random variables: A ~ U(0, 1), B ~ U(0, 1).
Calculate the following expected value: E(min(A, B)) = ?
Problem Solution
First and foremost, let’s define a random variable X = min(A, B) for our convenience.
Let’s recall the definition of expected value:
$$E(X)=\int_{-\inf}^{+\inf}xf(x)dx$$
where f(x) is the probability density function (PDF). While f(x) = F'(x), where F(x) is the cumulative distribution function (CDF).
This means that we can first find CDF F(x) → then find PDF f(x) → then find E(X). Sounds like a plan!
Starting with CDF:
$$\begin{aligned} F(x)&=P(X≤x)=1-P(X>x)=\\ &=1-P(min(A,B)>x)=1-P(A>x)*P(B>x)=\\ &=1-(1-x)^2 \end{aligned}$$
Next PDF:
$$f(x)=F'(x)=2(1-x)$$
And the last step:
$$\begin{aligned} E(X)&=\int_{0}^{1}2x(1-x)dx=2\int_{0}^{1}(x-x^2)dx=\\ &=2(\frac{x^2}{2}-\frac{x^3}{3})\Big|_{0}^{1}=\frac{1}{3} \end{aligned}$$
Hence, the answer is E(min(A, B)) = ⅓.
Conclusion
In this article, I’ve shown you how to solve maths problems from the interviews that can get you a job in Data Science. I can’t fail to mention that Data Science is an extremely promising field that opens up new opportunities for analyzing and processing large amounts of data. In Data Science projects, we work with fundamentally different types of data, apply various methods and algorithms, and create brand-new models and tools to solve urgent problems. However, without maths, there would be no Data Science. So, before you plunge into this rich field, you’ll have to pass an interview and solve simple yet treacherous maths problems, as shown above.
I hope you have solved these problems without looking into the solutions, and if so, go ahead – the magical world of Data Science is waiting for you!